Instabilities, Nonequilibrium and Active Behavior in Complex Fluids

by H. Pleiner
(external collaboration with W. Zimmermann, H.R. Brand, B. Huke, M. Lücke, D. Laroze, and D. Svenšek )

The investigation of instabilities of complex fluids under external fields is motivated by several important aspects. First, detection of the onset allows very precise measurements of relevant material parameters, which very often cannot be measured directly. Second, depending on the nature of the complex fluid, a host of different external fields, like electric and magnetic fields, temperature and concentration gradients, flow and mechanical fields, can be used to drive the system out of equilibrium. Third, in complex fluids even first instabilities can show non-trivial features, thus allowing a rather detailed theoretical description of complicated instability types as well as a quantitative comparison with experiments. Advanced topics are concerned with the spatial structures above onset, their defects and dynamics.

Topic A: smectic films under external electric fields are considered. The advantage of using films lies in their superior visualization properties and in the possibility to explore new geometries in the experimental setup. Generally, one can get instabilities within the layers (e.g. of nematic-like in-plane structures) as well as those of the layers (undulation or buckling).

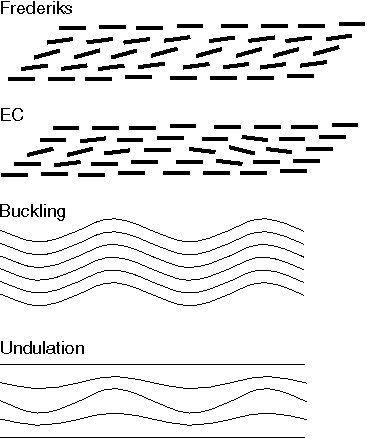
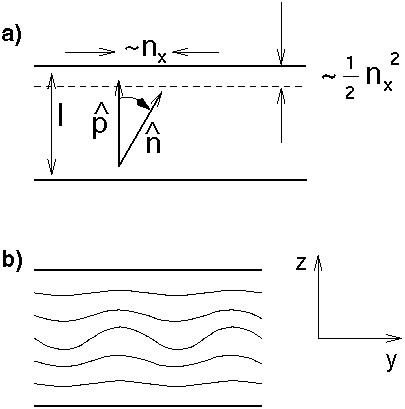
Topic B is related to shear induced reorientation of layered systems, like amphiphilic L_α phases, ordered block copolymers and smectic liquid crystals. We describe the onset of reorientation by a shear induced Helfrich-Hurault type instability using generalized hydrodynamic equations suitable for layered systems. Shear flow (in the x-direction, as shown below) tilts the director ˆn somewhat away from the layer normal ˆp, thus reducing the natural layer spacing. If the layer spacing is kept constant due to the experimental setup, this situation is equivalent to a dilation of the layers. Above a certain threshold undulational instability starts in the plane perpendicular to the shear plane, which eventually leads to a complete reorientation of the layers.

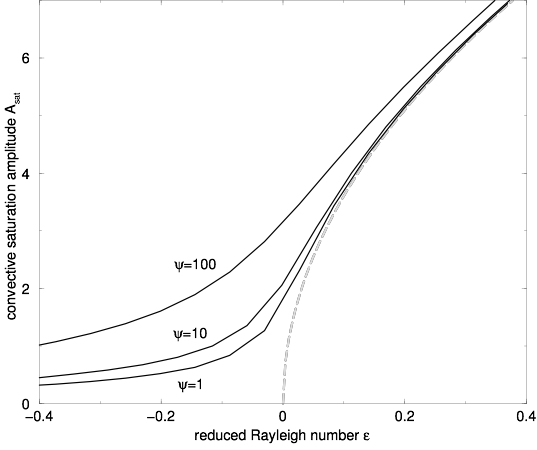
Topic C deals with (mostly thermal) instabilities in ferrofluids. Ferrofluids are dispersions of heavy solid ferromagnetic grains suspended in a carrier liquid. With a typical diameter of 10 nm the particles are pretty large on molecular length scales, resulting in an extremely small particle mobility (very small Lewis number L). This leads to a situation where de-mixing effects take place on time scales far beyond any reasonable observation time. On the other hand ferrofluids are characterized by a large thermo-diffusive or Soret effect (large separation ratio ψ). As a result of the joint action of thermal and solutal buoyancy forces (ψ>0) the critical Rayleigh number Ra_c for the onset of convection is dramatically reduced as compared to the pure-fluid reference value Ra⁰_c (for ψ=0). However, Ra_c is experimentally inaccessible due to the extremely slow growth of convection patterns, requiring extremely large observation times. For Rayleigh numbers of the order of Ra⁰_c (ε=0 in the Fig. below) an initially motionless configuration with a uniform concentration distribution grows to a finite amplitude convection pattern. This happens within a time, small compared to the creeping solutal diffusion time, but almost as fast as pure-fluid convection does above Ra⁰_c [A].

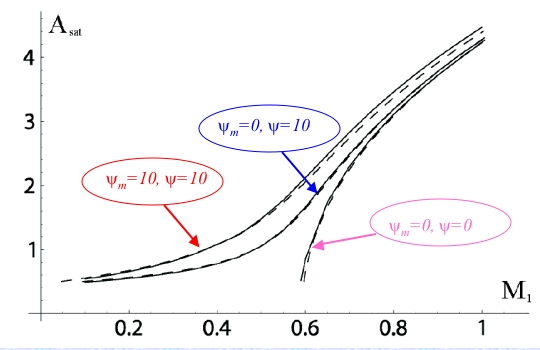
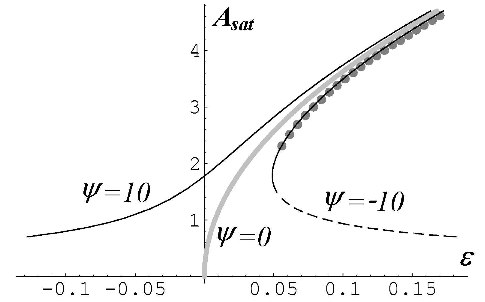
The influence of an external magnetic field on this bifurcation scenario is of experimental interest, since the field is an additional control parameter that is easily manipulated. The full system of hydrodynamic equations for magnetic binary mixtures is derived. Numerical calculation show that only two effects are important, Kelvin force and magnetophoresis. Another striking feature is the enhanced significance of the boundary layer due to the magnetic boundary condition. An approximate analytical solution of the boundary layer problem for concentration and magnetic potential is given. The bifurcation scenario (the saturation amplitude A_sat as a function of the external field) is shown below, where M₁ is proportional to the field intensity reflecting the Kelvin force. The dashed and solid curves are the analytical and numerical results, respectively; ψ_m is the magnetic separation ratio based on the concentration dependence of the magnetic susceptibility [B].

The case when the separation ratio (the Soret coefficient) is negative reveals a much richer variety of phenomena than that of positive separation ratio. In particular, for heating from below we find a linear oscillatory instability, whose amplitude, however, relaxes to zero on the long turn and is, thus transient only and, at higher Rayleigh numbers, a finite amplitude stationary instability coexistent with the linearly stable convection-free state (cf. below). By heating from above short-length-scale convective structures occur, whose wavelength depends on the Rayleigh number [C].

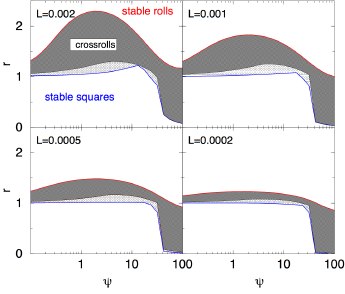
We investigate the bifurcation properties and pattern selection in Rayleigh-Bénard convecting binary mixtures for parameter combinations that are typical for colloidal fluids. We study stationary rolls, square and crossroll patterns for positive separation ratios. For colloids with positive separation ratios we found essentially the same sequence of stable structures as for molecular liquids with squares being stable at small reduced Rayleigh number r, rolls being stable at large r, and oscillatory and stationary crossroll patterns in between. For small Lewis number L the intervall where crossrolls exist is very small as long as ψ is smaller than 30 (cf. below). For negative separation ratios and Lewis numbers typical for colloidal solutions neither stable roll nor travelling wave convection is possible. [D].

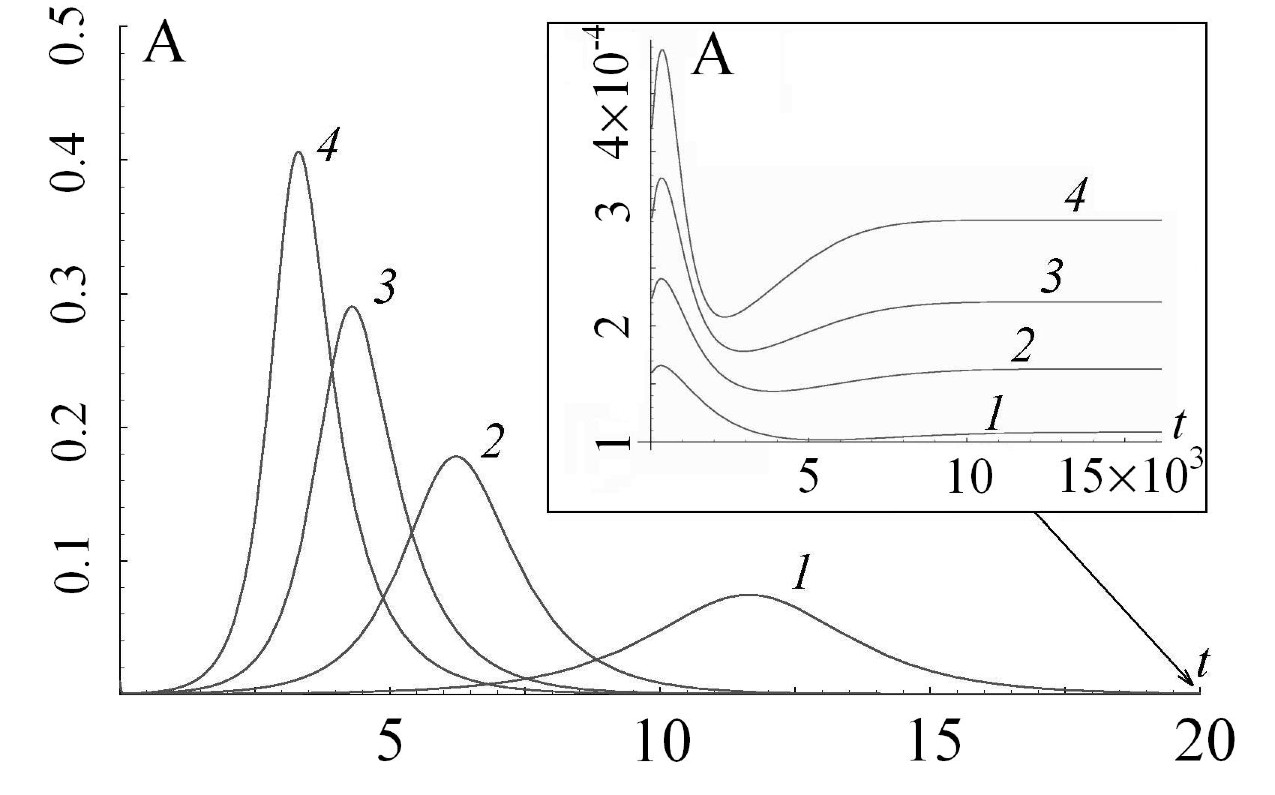
We describe a convective instability of a stratified ferrofluid subject to a magnetic field: In earth's gravity field, the density difference between particles and solvent is responsible for a sedimentation effect. Waiting long enough a concentration gradient evolves. If a strong enough external magnetic field is applied along the concentration gradient, instability sets in. The ferrofluid is described as a binary mixture featuring two important dimensionless numbers, B the barometric and B_m the magnetic barometric one. At the field strength, where the latter exceeds the former, instability sets in. We discuss [E] the growth rate of linear perturbations and the amplitude of nonlinear stationary convection rolls. Below, the amplitude of the velocity is shown as a function of time with B=100, and B_m= 150, 200, 250, 300 (curves 1-4, respectively). The inset magnifies the long time behavior. The latter is governed by the balance of concentration advection and sedimentation.

For a discussion of instabilities in ferronematics (thermal convection and Saffman-Taylor) and ferrogels and ferrofluids (Rosensweig), cf. also Unconventional Ferrofluids

Topic F: Active Systems:
Active systems are (predominantly) biological systems that are driven out of equilibrium, not by externally applied driving fields, but internally - typically by chemical reactions. As long as the internal driving forces are operating, the units of the active system move, and due to this motion an ordered spatial structure is created. Examples are schools of fish or flocks of birds, pattern forming growing bacteria, biological motors (myosin and actin), or general suspensions of active particles. If the internal drive stops, e.g. due to lack of nutrients, the system becomes passive, with no motion and no remaining localized collective spatial structures, anymore. Orientational order can be present through spontaneous breaking of a continuous symmetry in equilibrium systems, like in nematic and polar nematic liquid crystals. In these equilibrium systems, the spatial structure is static in nature. Similarly, static orientational order can be induced in some systems by strong external (magnetic or electric) fields or mechanical stresses. In both cases the spatial structure and its dynamics is described by a second rank orientational tensor (which can be used to define a director) or a polar vector. These quantities are static in the sense that they do not change under time reversal. It us rather popular to describe also active systems by those static quantities (and adding a so-called "active" term). However, we take a different point of view and describe the active structure as a dynamic one, created by the motion of active units. The natural candidate for the variable to describe the dynamic structure is then (in the polar case [F] ) the velocity and (in the non-polar case [G] ) the mean angular velocity of the active entities. Since there is generally also a non-active background motion (flowing water or solvent, windy air, etc.), there are two different velocities in the polar case. As a result, the hydrodynamics of these (polar) dynamically ordered systems shows, e.g., a normal mode structure quite different compared to the static descriptions, in particular an anisotropic first sound (impossible for equilibrium systems) and a propagating second sound (in equilibrium systems only possible for superfluids and for elastic media). In addition, there are linear couplings between (active) flow and e.g. densities and concentrations due to the genuine two-fluid transport derivatives. The very non-equilibrium nature of these systems is manifest by the existence of a non-zero (active) velocity even in the stationary limit. If this stationary active velocity goes to zero, the passive (equilibrium) state is reached - a transition that is described by well-known bifurcation scenarios. A simplified model on the basis of this dynamic order description has recently be used to successfully explain the stop-and-go dynamics of the growth front of Proteus mirabilis bacteria colonies [H]. Fig.1 shows stroboscopically the time evolution of the growth front, while Fig. 2 demonstrates the stop-and-go behavior.

Fig.1: